Path Planner for Highway Autonomous Driving

Objective

Implement a simple real-time path planner in C++ to navigate a car around a simulated highway scenario, including other traffic, given waypoint, and sensor fusion data.

The planned path should be safe and smooth, so that tha car avoids collisions with other vehicles, keeps within a lane (aside from short periods of time while changing lanes), and drive according to the speed limits (50mph). Besides, the car must not violate a set of motion constraints, e.g. maximum acceleration (10 m/s^2), and maximum jerk (50 m/s^3). As a results, the car is drive safely and the passengers feel comfortable.

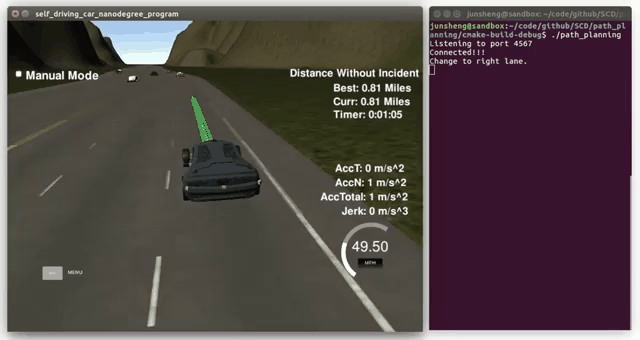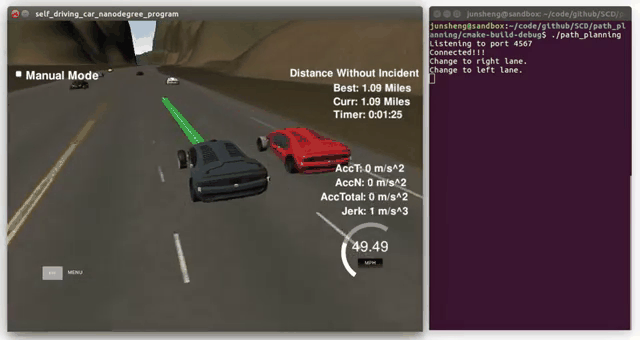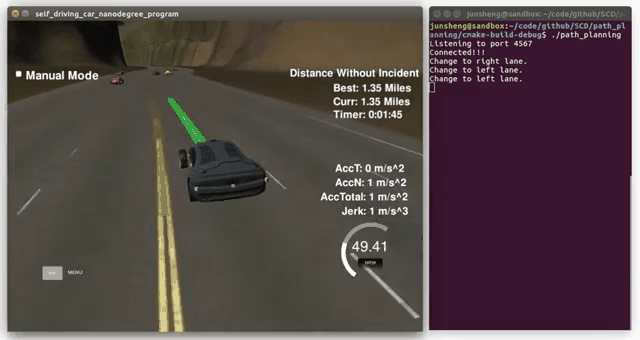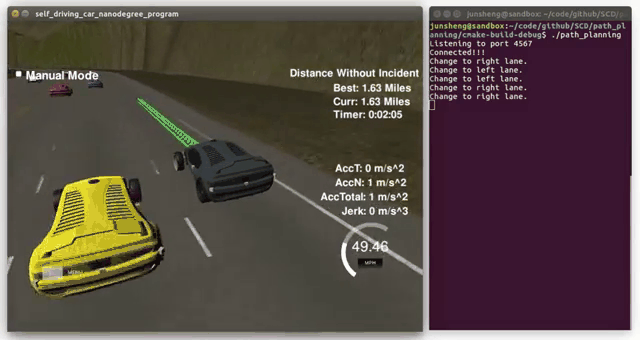
Demo (video playbacks 4-time faster than real)

(click to see the full video)

1 Code & Files

1.1 My project includes the following files and folders

src contains the source code.
data csv file for highway maps.
images contains examples.
install-uWebSockets contains the bash scripts to install uWebSockets.
CMakeLists.txt is the CMake file.

1.2 Dependencies & my environment

cmake >= 3.5
All OSes: click here for installation instructions
make >= 4.1
- Linux: make is installed by default on most Linux distros
- Mac: install Xcode command line tools to get make
- Windows: Click here for installation instructions
gcc/g++ >= 5.4
- Linux: gcc / g++ is installed by default on most Linux distros
- Mac: same deal as make - [install Xcode command line tools]((https://developer.apple.com/xcode/features/)
- Windows: recommend using MinGW
uWebSockets
- Run either install-mac.sh or install-ubuntu.sh.
- If you install from source, checkout to commit e94b6e1, i.e.
```
git clone https://github.com/uWebSockets/uWebSockets 
cd uWebSockets
git checkout e94b6e1
```

1.3 How to run the code

Clone this repo.
Make a build directory: mkdir build && cd build
Compile: cmake .. && make
Run it: ./path_planning.
Open the simulator, which is downloaded from here

1.4. Release History

0.1.1
- Added a few features and first proper release
- Date 1 January 2018
0.1.0
- Initiated the repo
- Date 11 December 2017

2 Approaches

2.1 Algorithm Steps

(1) Utilize the sensor fusion data to check each lane’s availability

Go through all the detected vehicle’s information and status, and check the availabilities of each lanes. See code from line 256-306 in src/main.cpp.

Note: [“sensor_fusion”] is a 2d vector of cars and then that car’s [car’s unique ID, car’s x position in map coordinates, car’s y position in map coordinates, car’s x velocity in m/s, car’s y velocity in m/s, car’s s position in frenet coordinates, car’s d position in frenet coordinates.

(2) Based on the lanes’ availability to plan the next state of the car

Choose one of the following states for the car, based on the lane’s availability which is obtained from the sensor fusion. See code from line 310-324 in src/main.cpp.

Change to left lane
Change to right lane
Keep lane (speed up, slow down or keep speed)

(3) Use anchor points to interpolate a spline curve

To create a smooth path, two last points from the previous planned path and another 3 predicted future points are used together for computing a smooth spline curve, which is visualized as planned path. Then break the entire spline curve into 50 points which is used to control the vehicle’s speed (our car visits them sequentially every 0.02 seconds). See code from line 332-443 in src/main.cpp.

Note: There will be some latency between the simulator running and the path planner returning a path, with optimized code usually its not very long maybe just 1-3 time steps. During this delay the simulator will continue using points that it was last given, because of this it’s a good idea to store the last points we have used so we can have a smooth transition.

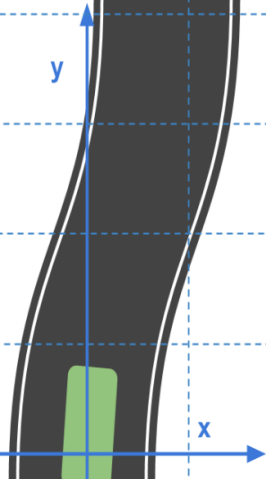
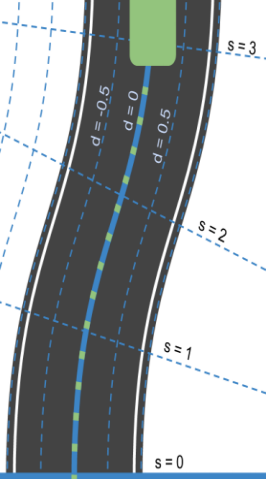
2.2 Frenet coordinates

Cartesian coordinates	Frenet coordinates	Benifits of Frenet

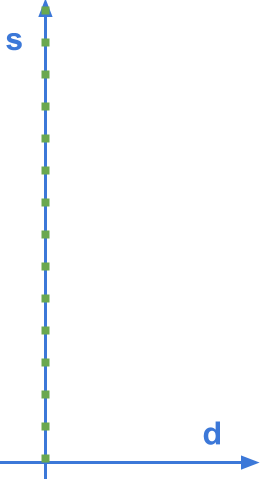Frenet coordinates make the math easy to describe the driving behaviors.

we use s=0 to represent the beginning of the segment of road.
We use d=0 to represent the center line of that road. To the left of the center line we have negative d and to the right d is positive.

3 Data format

3.1 The map of the highway is in data/highway_map.txt

Each waypoint in the list contains [x,y,s,dx,dy] values. x and y are the waypoint’s map coordinate position, the s value is the distance along the road to get to that waypoint in meters, the dx and dy values define the unit normal vector pointing outward of the highway loop. The highway’s waypoints loop around so the frenet s value, distance along the road, goes from 0 to 6945.554.

3.2 Main car’s localization Data

[“x”] The car’s x position in map coordinates

[“y”] The car’s y position in map coordinates

[”s”] The car’s s position in frenet coordinates

[“d”] The car’s d position in frenet coordinates

[“yaw”] The car’s yaw angle in the map

[“speed”] The car’s speed in MPH

3.3 Previous path data given to the Planner

//Note: Return the previous list but with processed points removed, can be a nice tool to show how far along the path has processed since last time.

[“previous_path_x”] The previous list of x points previously given to the simulator

[“previous_path_y”] The previous list of y points previously given to the simulator

3.4 Previous path’s end s and d values

[“end_path_s”] The previous list’s last point’s frenet s value

[“end_path_d”] The previous list’s last point’s frenet d value

4 Discussion

The autonomous car is able to complete loop around the 6946m highway without collisions with other vehicles and uncomfortable jerk, and its follows the road speed limits with gentle acceleration. Besides, the car is able to take over the slow vehicles when there are suitable opportunities, e.g. enough spacefs to both leading and following vehicles.

Currently, the lane changes algorithm is quite simple and to further improve the path planner, we can build a finite state machine to move between actions, and build a cost function to determine the best action.